Whaley Model

The quadratic approximation method by Baron-Adesi and Whaley (1987) can be used to price American options.

TheoV

Call

where

b – the cost-of-carry rate;

b = r            to price options on stocks.

b = r – q       to price options on stocks and stock indexes paying a continuous dividend yield q

b = 0            to price options on futures.

b = r – r_f       to price currency options (r_f – risk-free rate of the foreign currency).

C_GBS – the generalized Black-Scholes call TheoV expression;

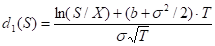
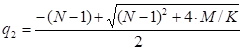
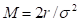
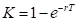
S^* – the critical commodity price for the call option that satisfies

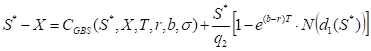
The last equation should be numerically solved to find S^*.

Put

where

P_GBS – the generalized Black-Scholes put TheoV expression;

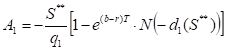
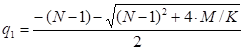
S^**– the critical commodity price for the put option that satisfies

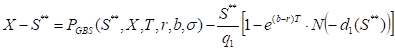
The last equation should be numerically solved to find S^**.

Delta

Call

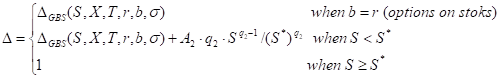
where

∆_GBS - the generalized Black-Scholes call ∆ expression.

Put

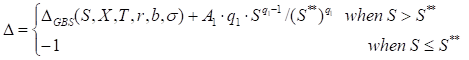
where

∆_GBS - the generalized Black-Scholes put ∆ expression.

Gamma

Call

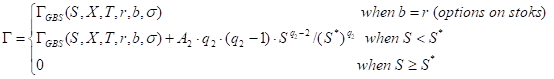
Put

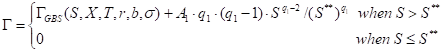
Vega

Call

Put

Theta

Call

where

Θ_GBS - the generalized Black-Scholes call Θ expression.

Put

where

Θ_GBS - the generalized Black-Scholes put Θ expression.

Rho

Call

where

ρ_GBS - the generalized Black-Scholes call ρ expression.

Put

where

ρ_GBS - the generalized Black-Scholes put ρ expression.

Implied volatility

System numerically finds implied volatility.

Implied volatility can’t be calculated for call option if option value is less than (underlying price - strike).

Implied volatility can’t be calculated for put option if option value is less than (strike - underlying).